Having access to an online game simulator is quite useful in teaching various aspects of statistics. We will look at three in order of complexity: a basic projectile simulator, a catapult and the trebuchet.
While using an online simulator loses the hands-on aspect and the associated errors, it relieves us of having to have the physical equipment needed. As such, it does have its uses in certain cases.
While such simulators can be used in most of the statistical applications found in training and statistical software, we will discuss those related to design of experiments. Our aim here is to introduce the simulators for use in experimental design training without going through the experimental designs or the analysis.
NOTE: Some online simulations use Adobe Flash, which no longer will be supported after 12/31/20. We have not included those.
In designing an experiment, there are three important principles to follow:
- Randomization
- Replication
- Blocking
However, in the deterministic simulations we will discuss, for a given setting, you will get the same result every time you run the simulation. As a result, the three basic principles for experimental design: randomize, replicate, and blocking do not apply.
Therefore, run any experimental design used in standard order. You will need to analyze the result as an unreplicated design. We’ll discuss that briefly after introducing all the simulators.
“Note the properties required by deterministic simulation render traditional design strategies – replication, randomization, and blocking – useless.”
Comparing Designs for Computer Simulations, Proceedings of the 2008 Winter Simulation Conference, pp. 463-470, Rachel T.Johnson, Douglas C. Montgomery, Bradley Jones, and John W.Fowler.
This is an excellent article which discusses more advanced designs suitable for computer experiments. It is beyond the scope of this blog.
On to the online simulators.
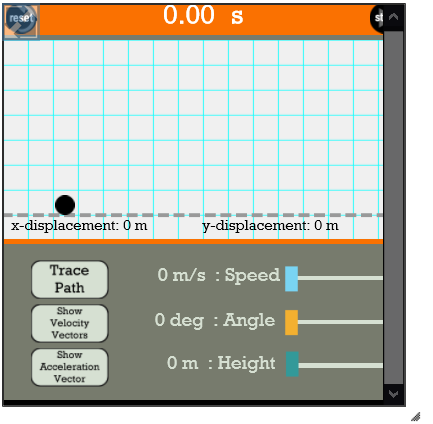
The Projectile Simulator
Designed for teaching physics from the Physics Classroom , the Projectile Simulator with three inputs and two outputs provides a nice platform for simple experimental design exercises.
You can access the simulator here.
Once there click on Launch Interactive. This is the link that will appear: https://www.physicsclassroom.com/Physics-Interactives/Vectors-and-Projectiles/Projectile-Simulator/Projectile-Simulator-Interactive
Read the instructions to expand to full screen or size to your liking.
The three inputs are
- Speed: Projectile launch speed, 0 to 60 meters/second
- Angle: Launch angle: 0 to 90 degrees
- Height: Height at launch: 0 to 120 meters
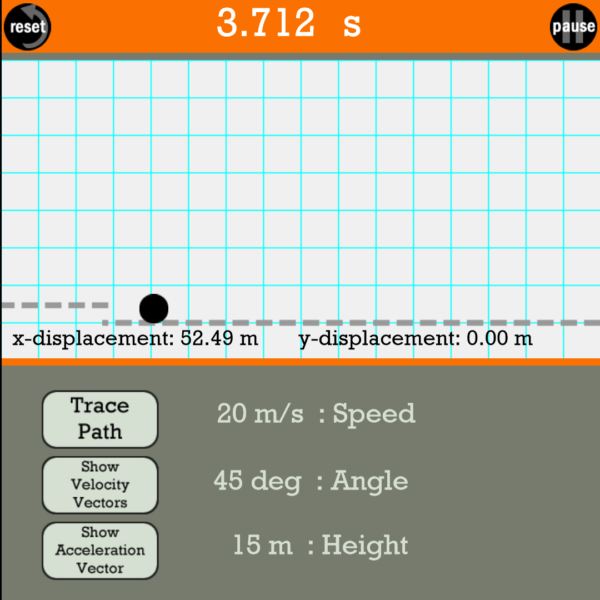
There are two outputs: x-displacement and y-displacement. We will use the final x-displacement as our response. We would like to find the settings that maximize it.
Here is an example run:
The Catapult
SigmaZone training and consulting company has virtual single cup and double cup catapult simulators free for individual and commercial use. They can be run either as a deterministic simulation or as a stochastic one.
They can be accessed here.
We’ll discuss the single cup catapult in deterministic mode.
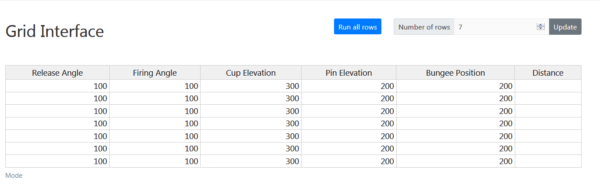
There are five inputs and one output: distance. Click on Show Tips to see how to adjust the settings.
We recommend, as does SigmaZone, that you use the Catapult grid to record and run your settings. This is the grid for the single cup catapult.
Notice Mode at the lower left hand corner. Here you can choose either Deterministic or Stochastic.
We will choose Deterministic for our focus on unreplicated designs.
Here are the minimum and maximum settings for the five inputs:
- Release Angle: 100 to 185
- Firing Angle: 90 to 140
- Cup Elevation: 200 to 300
- Pin Elevation: 100 to 200
- Bungee Position: 100 to 200
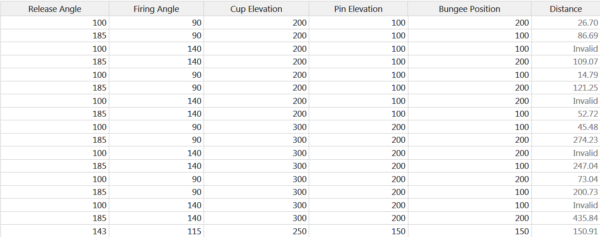
For discussion, we set up a 16 run, resolution V design in five factors with one center point since we are using the deterministic mode. Here is the design in standard order with the result.
Note: there are some settings which are marked “Invalid.” This happens in real situations when some combinations can’t be run or lead to unwanted results. Such results lend themselves to a discussion of what to do in the analysis.
We won’t go into the analysis of the above data here. However, note that the maximum/minimum response is greater than 10 which means a Box-Cox transformation chosen optimally during regression could be useful.
One could also use the catapult for a more advanced approach. Space filling designs are recommended for computer simulations and we have a constrained region since some settings are invalid. Discussing this approach is beyond the scope of this blog.
NOTE: If you choose Stochastic mode, then randomization, replication and blocking apply.
The Virtual Trebuchet
Our final virtual simulation is the virtual trebuchet. It can be found here.
This is a quite complex deterministic simulation with many potential variables.
You will need to do some study to become familiar with its use. You can fix some of the variables and only allow others to vary, for example. You should be able to use this simulation for screening, characterization, and optimization.
Analysis of Unreplicated Designs
Having introduced you to these three simulators as deterministic simulations, we will say a few things about the analysis of unreplicated designs.
Using a deterministic online simulator for experimental design does present a problem in the analysis as there is no experimental error to judge important effects due to the lack of replication.
By removing some terms in the model, those terms go into experimental error which you can then use to judge the significance of effects. But which term(s) should be removed?
This is a well-known issue associated with unreplicated designs, and there have been several approaches to the solution.
Normal and half-normal probability plots and Lenth’s pseudo standard error are two of the older established approaches.
In an excellent video, Philip Ramsey, Senior Data Scientist and Statistical Consultant at Predictum, Inc. uses SAS/JMP 12 to discuss how to analyze unreplicated designs. While the mechanics of the analysis are in JMP, the overall points he makes at each step can be implemented in other statistical software, such as Minitab. He mentions both the half-normal probability plot and Lenth’s Pseudo Standard Error as methods to start choosing which terms to remove from the model.
You can view Philip’s video here.










Leave A Comment